1. Что такое статистическая гипотеза?
2. Статистические гипотезы - примеры
3. Нулевые и альтернативные гипотезы
4. Зачем формулировать статистические гипотезы?
5. Статистические гипотезы - ошибка первого типа
6. Уровень серьезности
7. Тест мощности
8. Таблица ошибок
9. Статистическая проверка гипотез
10. Тестовая статистика
11. Статистические гипотезы - критическая область
12. Виновный или невиновный
13. Статистические гипотезы - пример Янины
14. Ежики и дафнии - описание проблемы
15. Статистические гипотезы - этапы проверки
16. вход
17. Нулевые и альтернативные гипотезы
18. Проверка гипотезы
19. Что такое р-значение?
20. Статистические гипотезы - резюме

Некоторые говорят, что статистические гипотезы - простая и приятная тема. Я не могу согласиться с этим. Я помню, как перепутали нулевую и альтернативную гипотезы и ошибку первого типа со ошибкой второго типа. К этому добавилось таинственное значение p-значения, и я вообще ничего не понял. Почему мы никогда не принимаем нулевую гипотезу и ищем только основания для ее отклонения? Что такое тестовая мощность и уровень значимости? Какова критическая область? Слышите ли вы красный свет на своей голове, когда услышите эти вопросы, и хотите ли вы кричать ЖИЗНЬ? Если это так, я действительно надеюсь, что после прочтения статьи ниже лампа станет зеленой, и крик «спасение» изменится на «уффф ... статистические гипотезы не так уж плохи».

Что такое статистическая гипотеза?

Статистическая гипотеза - это утверждение о распределении население , Это может относиться либо к его функциональной форме (то есть к какому распределению относится статистическая совокупность - обычно проверяется нормальное распределение), либо к значениям параметров (обычно к среднему арифметическому).

Статистические гипотезы - примеры

Примеры статистических гипотез, конечно, можно умножить, и каждый может быть интереснее предыдущего. Позвольте мне представить вас здесь, чтобы вы могли знать, какие статические гипотезы вы можете изобрести сами:

• средний рост поляков составляет 175 см
• 30% людей говорят по-английски
• 2% детей школьного возраста не любят шоколад
• уровень счастья через две минуты после употребления большой порции мороженого выше, чем до употребления такой порции мороженого
• Люди, которые занимаются спортом, более здоровы, чем люди, которые избегают физических упражнений
• кассир всегда движется медленнее, если я стою в нем

Нулевые и альтернативные гипотезы

Мы уже знаем, что такое статистические гипотезы. Мы можем привести разные примеры. Стоит познакомиться с понятием нулевых и альтернативных гипотез сейчас.

Нулевая гипотеза , в упрощении, гласит, что нет никакой разницы. Поэтому (принимая во внимание один из приведенных выше примеров) мы можем сказать, что перед тем, как съесть большую порцию мороженого, мы так же счастливы, как и после того, как съели этот десерт. Нет разницы в уровне нашего ощущения счастья, мороженое не влияет на настроение.

Мы формулируем альтернативную гипотезу с нулевой гипотезой. Альтернативная гипотеза говорит, что разница, однако, есть. Уровень счастья варьируется в зависимости от того, едите ли вы большую порцию мороженого или нет. Мы можем сформулировать это тремя различными способами:

1. Уровень счастья перед едой мороженого и после еды у них разный.
2. Уровень счастья после употребления мороженого выше, чем до его употребления.
3. Уровень счастья перед употреблением мороженого выше, чем уровень счастья после употребления десерта.

Зачем формулировать статистические гипотезы?

Цели формулирования статистических гипотез могут быть разными. Все зависит от исследований, которые мы проводим. Ниже приведены некоторые примеры.

• исследование предположений относительно среднего уровня черт в популяции - например, мы проверяем данные о среднем росте населения, мы изучаем средний вес печенья или шоколада
• оценка различия между двумя группами - например, мы проверяем, являются ли женщины и мужчины такими же спортивными, мы проверяем гипотезу о том, что учащиеся в частных и государственных школах имеют одинаковые оценки
• изучение зависимости между особенностями - например, мы проверяем, зависит ли хорошее настроение от количества съеденного мороженого
• сравнение распределений переменных - чаще всего мы исследуем, имеет ли наблюдаемый признак нормальное или почти нормальное распределение

Статистические гипотезы - ошибка первого типа

Первый тип ошибки - это когда мы отвергаем нулевую гипотезу, и это было правдой. Так что, если это будет так, что уровень счастья после употребления большой порции мороженого не изменится полностью, и мы на самом деле так же счастливы, как перед едой, и мы отвергаем эту гипотезу для альтернативной гипотезы, что уровень счастья уменьшается (из-за этого ужасного раскаяния, что опять же слишком много калорий и вам понадобится два часа на тренировки), мы сделаем ошибку первого рода. Потому что мы отвергли нулевую гипотезу, которая была правдой.

Уровень серьезности

Вероятность совершения ошибки первого типа в ситуации, когда нулевая гипотеза была верной, определяется символом α (альфа), и мы называем его уровнем значимости.

Уровень значимости определяет максимальный риск совершения ошибки первого типа, которую мы готовы принять. Выбор значения α зависит от человека, проводящего исследование, от характера проблемы и от того, как именно мы хотим проверить ваши гипотезы. Наиболее часто предполагаемым является α = 0,05. Другие популярные значения - 0,1, 0,01 или даже 0,001.

Второй тип ошибок возникает, когда мы не отвергаем ложную гипотезу. Это происходит в ситуации, когда, однако, этот уровень счастья перед едой мороженого и после еды отличается. Если эти угрызения совести из-за высокого потребления калорий настолько серьезны, что, несмотря на то, что мы едим что-то хорошее и вкусное, мы не чувствуем себя лучше. И если уровень счастья определенно снижается после употребления мороженого, и мы обнаруживаем, что разницы нет, то мы совершаем ошибку второго рода. Мы не отвергаем нулевую гипотезу, даже если она неверна.

Вероятность ошибок второго типа определяется символом β (бета).

Ограничение второго типа ошибок очень важно в некоторых тестах. Например, в случае с лекарством лучше сказать здоровому пациенту сделать дополнительный тест (когда в случае нулевой гипотезы - пациент здоров - мы ошибочно заподозрили заболевание), чем отправить больного домой без лечения с информацией о том, что он здоров (ошибка второго типа) ,

Тест мощности

Мощность теста (вероятность того, что мы правильно отвергнем нулевую гипотезу) равна 1-β. Другими словами, это вероятность несоблюдения ошибки типа II.

Мощность теста зависит от нескольких факторов:

1. Размер образца, используемого в тесте (чем больше образец, тем больше мощность теста).
2. Фактический размер эффекта на фоне случайных вариаций в популяции.
3. Принятый уровень значимости α (между типом ошибки I и типом II есть такая зависимость, что, если мы увеличиваем вероятность совершения данной ошибки, мы одновременно уменьшаем ее для другой).

Таблица ошибок

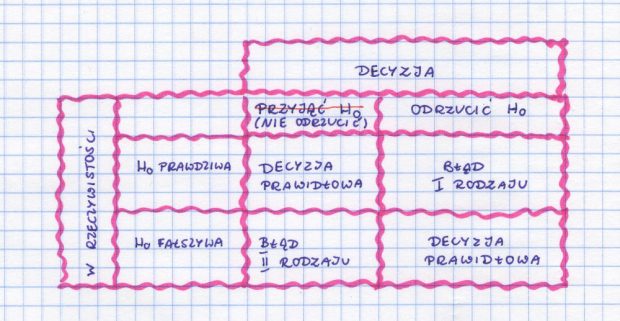
таблица: тип I и тип ошибки II

Статистическая проверка гипотез

Статические проверки гипотез - это такие действия, которые направлены на то, чтобы отвергнуть или не отвергнуть гипотезу. Мы делим тесты на параметрические и непараметрические (соответствие). Примерами непараметрических гипотез являются форма распределения переменных или случайность выборки. Выбор теста связан с выбором соответствующей шкалы измерения (интервал, порядковый, номинальный - для тех, кто заинтересован, я ссылаюсь на статью о разделение функций по Стивенсу ) представлены проанализированные данные и выбор модели исследования. Мы можем иметь дело с зависимой или независимой моделью. Зависимым является то, когда измерения связаны друг с другом, они выполняются несколько раз для одних и тех же объектов. Независимая модель - это модель, когда мы проводим несвязанные измерения на объектах, принадлежащих к разным группам.

Тестовая статистика

Это функция попытки, на основании которой человек отвергает или не предлагает статистическую гипотезу.

Упрощение: на основе имеющихся у нас данных (например, размер выборки, ее распределение, тип данных и т. Д.) Мы выбираем, какие формулы мы будем использовать в наших расчетах.

Статистические гипотезы - критическая область

Область всегда расположена в конце распределения. Если вычисленное нами значение тестовой статистики находится в этой области, мы отвергаем нулевую гипотезу, которую проверяем. Размер критической области определяет сколь угодно малый уровень значимости α, тогда как ее местоположение определяется альтернативной гипотезой.

Чаще всего похоже, что мы рисуем диаграмму распределения и отмечаем штрихи под диаграммой, в какой области мы отвергнем нулевую гипотезу. Если нулевая гипотеза говорит о том, что что-то отличается, то критическая область является двусторонней, и мы отмечаем как правый, так и левый концы распределения. Если альтернативная гипотеза сформулирована как меньшая или большая, мы отмечаем область отскока либо справа, либо слева от нашего изображения.

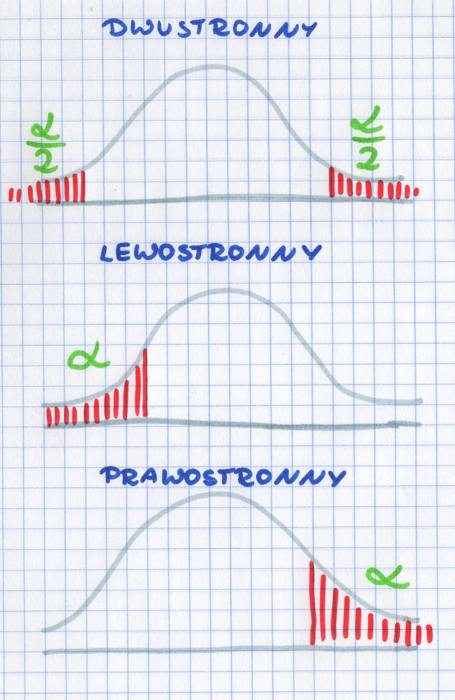
статистические гипотезы: критическая область

Виновный или невиновный

Пример судебного иска может помочь нам понять, когда мы принимаем альтернативную гипотезу и почему отказ от принятия альтернативной гипотезы не означает, что мы принимаем нулевую гипотезу.

Представьте, что мистер X обвиняется в краже алмаза миссис Y. Мистер X находится в суде. Нулевой гипотезой в этом случае является невиновность мистера X. Мы предполагаем, что мистер X не крал эти алмазы, что уборщик, повар или миссис Y спрятали их в другом ящике и забыли об этом. Альтернативная гипотеза, конечно же, вина г-на X. Если он не невиновен, это означает, что он украл алмазы и должен быть осужден судом. Однако предпосылкой для этого является отсутствие вины - суд должен найти убедительные аргументы, чтобы мистер Х мог обвинить вас. Если он их находит - это означает, что он отвергает нулевую гипотезу (ту, что касается невиновности) в пользу альтернативной гипотезы (что г-н Х виновен в совершении преступления). Если аргументы отсутствуют, то (даже если суд по-прежнему подозревает, что что-то в поведении г-на Х не соответствует и что эта невиновность вовсе не бесспорна), нет оснований отвергать нулевую гипотезу. Это не означает, что г-н Х не украл алмазы. Это просто означает, что суд не нашел достаточно доказательств.

Где здесь ошибки? Если г-н Х украл алмазы и был осужден, суд не допустил ошибки. Если он не украл алмазы и не был признан виновным, он также не ошибся. Если он не украл и отправился в тюрьму, мы имеем дело с ошибкой первого рода. Однако если г-н Х украл алмазы и был оправдан, то мы имеем дело со вторым типом ошибки.

Статистические гипотезы - пример Янины

Может ты знаешь Янина Дейл у, и если вы этого не знаете, это определенно стоит узнать. Янина очень хороший человек, и, возможно, именно поэтому она позволила мне использовать ее перевод, каковы статистические гипотезы и ошибки первого и второго рода. Пример основан на борщевиках и дафниях (и первоначально появился где-то в комментариях на Facebook, и поскольку такие комментарии обычно имеют короткую жизнь, мне было их очень жаль). И у кого не будет этого единственного примера Джанина, я приглашаю вас к записи: http://janinadaily.com/trudne-zycie-i-jeszcze-gorsze-metafory/ , В этой записи вы можете прочитать перевод ошибки второго типа на примере овцы и фермера, а также на примере теста на беременность. Но давайте вернемся к болотам и дафнии, и я на мгновение озвучу Джанину ...

Ежики и дафнии - описание проблемы

Ошибка типа II связана с мощностью теста, который мы также можем контролировать, например, выбрав правильное количество борщевика и дафнии. Сколько животных мы должны рассказывать анекдотам, что наши выводы точны и достоверны, тоже можно посчитать. Я не считал, потому что я немного здесь говорю в целом, но может оказаться, что 100 Дафний и 100 Хеджеров слишком малы, и тогда, чтобы быть уверенными в том, что наши выводы верны, мы должны пойти и рассказать анекдоты другим домашним животным.

Статистические гипотезы - этапы проверки

1. Формулировка предположений исследования
2. определение нуля и альтернативных гипотез
3. выбор тестовой статистики
4. выбор уровня значимости
5. определение критической области
6. расчет статистики по выборке
7. решение на основе расчетов
8. делать выводы в контексте проведенного исследования

Статистические гипотезы - пример проверки

Пусть не будет того, что вся статья является просто теорией, я решил показать один упрощенный пример того, как выглядит проверка статистической гипотезы.

вход

Предположим, я пошел в магазин, чтобы купить мой любимый 100-граммовый шоколад. Поскольку я завтракал утром, мне удалось принести шоколад домой. Ну, я решил взвесить его и с ужасом обнаружил, что моя плитка шоколада весит не 100 грамм, а 95 грамм. Могу ли я с полной уверенностью сказать, что все плитки шоколада имеют такой способ? Что я заведомо обманут производителем шоколада? Возможно, этот шоколад - результат ошибки, а все остальные весят столько, сколько должны. Возможно, однажды я получу шоколад весом 95 грамм, а в другой раз весом 107 грамм.

Нулевые и альтернативные гипотезы

Так что стоит проверить, как выглядит ситуация. Я решил проверить статистическую гипотезу, что купленный шоколад весит слишком мало.

Моя нулевая гипотеза предполагает, что производитель прав: шоколад весит ровно 100 грамм.

\ (H_ {0}: \ overline {x} = 100 \)

Альтернативная гипотеза состоит в том, что шоколад весит менее 100 граммов (я проверю левую гипотезу).

\ (H_ {A}: \ overline {x}

В качестве уровня значимости я решаю принять α = 0,05.

Проверка гипотезы

Чтобы проверить свою гипотезу на 100 дней, я покупаю и взвешиваю шоколад. Однажды я получаю меньше 100 грамм, иногда больше. Через 100 дней мне приходит в голову, что средний вес шоколада составляет 98 грамм. Есть ли у меня повод для беспокойства? Это не так много, как мои 95 грамм в первый день, но все же меньше, чем 100 грамм, что написано на упаковке.

В начале я рассчитываю стандартное отклонение - предположим, что это 5.

Тогда я считаю стандартную ошибку:

\ (SE = \ гидроразрыва {s} {\ SQRT {п}} \)

В нашем случае стандартная ошибка равна ½.

Я использую формулу: \ (Z = \ frac {\ overline {x} -μ} {SE} \)

Z = -4

Используя таблицу нормального распределения для α = 0,05, мы читаем значение -1,645. Наша статистика имеет левостороннюю критическую область (из-за альтернативной гипотезы, что шоколад весит менее 100 грамм). -4 меньше -1,645, и поэтому мы отвергаем нулевую гипотезу для альтернативной гипотезы. Таким образом, мы отвергаем нулевую гипотезу, что шоколад весит 100 грамм, для альтернативной гипотезы, что они весят менее 100 грамм. Мы не можем быть на 100% уверены, но наши наблюдения предоставили нам такие доказательства, которые убедили нас отвергнуть нулевую гипотезу с вероятностью допустить ошибку первого типа (что означает, что шоколад весит 100 граммов) 5%.

Что такое р-значение?

P-значение - это совокупная вероятность взятия выборки, или более экстремальная, как наблюдалось, при условии правильности нулевой гипотезы.

Если значение p ниже уровня статистической значимости, ранее принятого нами, можно поступить так, как если бы нулевая гипотеза была отвергнута.

Вы можете прочитать немного больше о p-значении в блоге. Статистическая Чрезвычайная ситуация или Статистика в психологии ,

Статистические гипотезы - резюме

Статистические гипотезы являются темой реки. Чтобы исчерпать это, вам нужно больше, чем одна статья в блоге. Но я надеюсь, что эта статья сделает вас на один шаг ближе к пониманию того, что это такое.

А пока приглашаю вас прочитать другие статьи ( оглавление ) и к статистической привязанности facebook ,

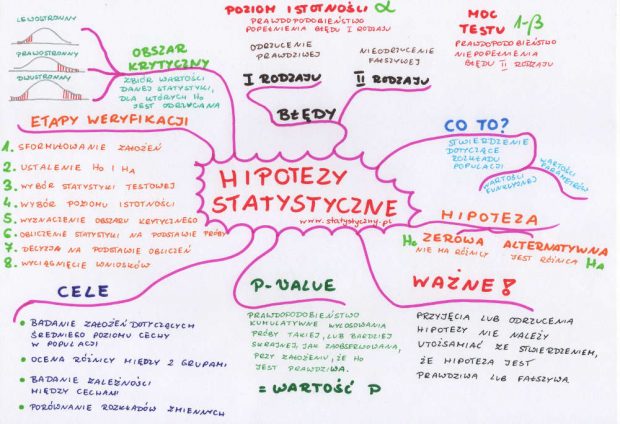
карта разума: статистические гипотезы

Пожалуйста, следуйте и нам нравится: